2019년07월20일 9번
[보관하역론] A사는 현재 2곳의 공장에서 다른 제품을 생산하여 3곳의 수요처에 각각 제품을 공급하고 있다. 물류센터 한 곳을 신축하여 각 공장에서는 물류센터로 운송을 하고, 물류센터에서 3곳의 수요처로 운송할 계획이다. 물류센터와 기존시설과의 예상되는 1일 운송빈도는 아래 표와 같으며, 거리는 직각거리(Rectilinear Distance)로 가정한다. 총 이동거리(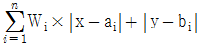 
)를 최소화시키는 신규 물류센터의 최적 위치는?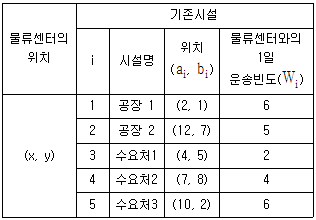
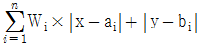)를 최소화시키는 신규 물류센터의 최적 위치는?- ① (x, y) = (6.0, 4.0)
- ② (x, y) = (6.2, 3.6)
- ③ (x, y) = (7.0, 2.0)
- ④ (x, y) = (7.0, 5.0)
- (x, y) = (7.8, 3.7)
(정답률: 22%)
문제 해설
이 문제는 최적화 문제로, 총 이동거리를 최소화하는 물류센터의 위치를 찾는 것이 목적이다. 이를 위해 직각거리를 이용하여 각 공장과 수요처 간의 거리를 계산하고, 이를 이용하여 총 이동거리를 계산한다. 이때, 물류센터의 위치가 바뀌면 각 거리가 달라지므로, 이를 반복적으로 계산하여 최적의 위치를 찾는다.
위의 보기에서 "(x, y) = (7.0, 2.0)"이 정답인 이유는, 이 위치에서 총 이동거리가 가장 작기 때문이다. 다른 보기들과 비교해보면, "(x, y) = (6.0, 4.0)"과 "(x, y) = (7.0, 5.0)"은 수요처들이 모두 오른쪽에 위치해 있어서 이동거리가 더 길어지고, "(x, y) = (6.2, 3.6)"과 "(x, y) = (7.8, 3.7)"은 공장과 수요처들이 대각선 방향에 위치해 있어서 이동거리가 더 길어진다. 따라서, "(x, y) = (7.0, 2.0)"이 최적의 위치이다.
위의 보기에서 "(x, y) = (7.0, 2.0)"이 정답인 이유는, 이 위치에서 총 이동거리가 가장 작기 때문이다. 다른 보기들과 비교해보면, "(x, y) = (6.0, 4.0)"과 "(x, y) = (7.0, 5.0)"은 수요처들이 모두 오른쪽에 위치해 있어서 이동거리가 더 길어지고, "(x, y) = (6.2, 3.6)"과 "(x, y) = (7.8, 3.7)"은 공장과 수요처들이 대각선 방향에 위치해 있어서 이동거리가 더 길어진다. 따라서, "(x, y) = (7.0, 2.0)"이 최적의 위치이다.
